Sinus und Cosinus
3HTAM Mathe-Hilfe online
Sinus und Cosinus
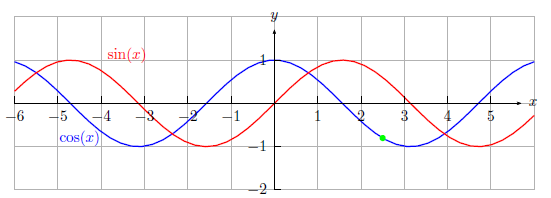
Die Sinus- und Cosinusfunktion sind nicht nur sehr ähnlich zu einander (Phasenverschiebung), sondern haben auch einen Zusammenhang bei der Ableitung. Wenn man sich die beiden Funktionen ansieht, beobachtet man, dass wenn einer der Beiden einen Extrempunkt hat; also mit anderen Worten die Steigung 0 ist; hat die andere Funktion einen Nulldurchgang. Nun wollen wir uns auf einen einzelnen Punkt $(x_0|\cos(x_0)$ konzentrieren. Beispielsweise den grün eingezeichneten Punkt $(2{,}5|\cos(2{,}5))$. Dieser Punkt liegt unterhalb der $x$-Achse. Schaut man sich nun den die Sinusfunktion an dieser Stelle an, so bemerkt man, dass diese eine negative Steigung besitzt. Diese Gemeinsamkeit gilt für diese beiden trigonometrischen Funktionen immer. \begin{align} \text{Gilt } \cos(x_0) \leq 0 \text{ , so folgt } \sin' (x_0) \leq 0. \\ \text{Gilt } \cos(x_0) \geq 0 \text{ , so folgt } \sin' (x_0) \geq 0. \end{align} Nicht nur das Vorzeichen stimmt überein, sondern auch die Funktionswerte. Man kann beweisen, dass $\sin'(x_0)= \cos (x_0)$ gilt. Diesen Beweis lassen wir an dieser Stelle aber außen vor. Auch für die Steigung der Cosinusfunktion können wir ein ähnliches Bild beobachten. Fällt die Cosinusfunktion, wie zum Beispiel beim grün eingezeichneten Punkt, so hat die Sinusfunktion dort einen positiven Funktionswert. Es lassen sich die folgenden beiden Ableitungsregeln aufstellen:
Ableitung vom Sinus und Cosinus
Für die Ableitungsfunktionen der Sinus- und Cosinusfunktion gilt:
\begin{align}
\sin'(x) &= \cos(x) \\
\cos'(x) &=- \sin(x)
\end{align}

Wir sehen, dass die Ableitungen zyklisch verlaufen, also immer im Kreis. Häufig hat man die beiden Funktionen nicht in der normalen Form vorliegen, sondern zum Beispiel so: \[ f(x) = \sin\left(x^2\right) \quad \text{oder} \quad g(x) = \cos(2x+4) \] Hier müssen wir die Kettenregel anwenden. Also innere mal äußere Ableitung. Somit ergeben sich für unsere beiden Beispielfunktionen die Ableitung: \begin{align} & f'(x)= \underbrace{2x}_{innere} \cdot \underbrace{\cos(x^2)}_{äußere} = 2x \cos\left(x^2\right) \\ & g'(x)= \underbrace{2}_{innere} \cdot \underbrace{(-\sin(2x+4))}_{äußere} = -2 \sin(2x+4) \end{align}
Wiederholung einiger Eigenschaften
In diesem Abschnitt haben wir bisher über die Ableitung der trigonometrischen Funktionen gesprochen. Nun wollen wir noch einmal kurz
alles Wissenswerte über die Funktionen darstellen. Ich hoffe diese Punkte sind aus der Mittelstufe noch einigermaßen geläufig,
da dies nur eine kleine Übersicht sein soll. (Hinweis: $k \in \mathbb{Z}$ für die Tabelle):
An dieser Stelle möchte ich auch nochmal an die Definition des Tangens erinnern:
Zuletzt gehen wir ein klein wenig auf die veränderten Sinus- und Cosinusfunktionen ein. Hierbei behandeln wir nur die
Sinusfunktion, da für die Cosinusfunktion dieselben Eigenschaften folgen.
Wertebereich: Den Wertebereich einer Sinusfunktion kann man mittels Vorfaktor verändern. So hat zum Beispiel die Funktion $2 \sin (x)$ einen Wertebereich $\mathbb{W}$ von $-2$ bis 2.
Nullstellen: Haben wir zum Beispiel die Funktion $\sin(x^2)$ und wollen die Nullstellen bestimmen, so suchen wir die $x$-Werte für die gilt $x^2 = k \cdot \pi$ gilt. Also in diesem Fall $\sqrt{k \pi}$.
Periode: Die Periode verändert sich auch mit dem Ausdruck im Inneren des Sinus. Zum Beispiel ist die Periodizität von $\sin (cx-d)$ gerade $\frac{2 \pi}{\left|c\right|}$. Wir nehmen den Betrag, da die Periodizität eine positive Länge ist. Das $d$ bedeutet nur eine (Phasen-)Verschiebung um $d$ Einheiten in $x$-Richtung.
Zuletzt ist noch folgende Identität von großer Bedeutung.
| $\mathbb{D}$ | $\mathbb{W}$ | Nullstellen | Def.-Lücken | Symmetrie | Periode | |
|---|---|---|---|---|---|---|
| $\sin x$ | $\mathbb{R}$ | $[-1,1]$ | $k \cdot \pi$ | keine | punktsym. | $2\pi$ |
| $\cos x$ | $\mathbb{R}$ | $[-1,1]$ | $\frac{1+2k}{2} \cdot \pi$ | keine | achsensym. | $2\pi$ |
| $\tan x$ | $\mathbb{R} \setminus \{\frac{1+2k}{2}\pi\}$ | $\mathbb{W}$ | $k \cdot \pi$ | $\{\frac{1+2k}{2}\pi\}$ | punktsym. | $\pi$ |
An dieser Stelle möchte ich auch nochmal an die Definition des Tangens erinnern:
Tangens
Der Tangens an der Stelle $x \in \mathbb{R} \setminus \{\frac{1+2k}{2}\pi\}$ ist definiert als
\[ \tan (x) = \frac{\sin (x)}{\cos (x)}. \]
Wertebereich: Den Wertebereich einer Sinusfunktion kann man mittels Vorfaktor verändern. So hat zum Beispiel die Funktion $2 \sin (x)$ einen Wertebereich $\mathbb{W}$ von $-2$ bis 2.
Nullstellen: Haben wir zum Beispiel die Funktion $\sin(x^2)$ und wollen die Nullstellen bestimmen, so suchen wir die $x$-Werte für die gilt $x^2 = k \cdot \pi$ gilt. Also in diesem Fall $\sqrt{k \pi}$.
Periode: Die Periode verändert sich auch mit dem Ausdruck im Inneren des Sinus. Zum Beispiel ist die Periodizität von $\sin (cx-d)$ gerade $\frac{2 \pi}{\left|c\right|}$. Wir nehmen den Betrag, da die Periodizität eine positive Länge ist. Das $d$ bedeutet nur eine (Phasen-)Verschiebung um $d$ Einheiten in $x$-Richtung.
Zuletzt ist noch folgende Identität von großer Bedeutung.
Sinus-Cosinus-Identität
\[ \sin^2(x) + \cos^2(x) = 1 \]