Orientierte Fläche
3HTAM Mathe-Hilfe online
Orientierte Fläche
Die Integralrechnung ist neben der Differentialrechnung einer der wichtigsten Teile der Analysis. Sie entstand aus dem Problem der Flächenberechnung, hat aber nicht
nur dort ihren Einsatz. Bei mehrdimensionalen Funktion, kann man so ein Volumen bestimmen.
Anders als bei der Differentialrechnung, wo man einen Algorithmus zum Ableiten angeben konnte, gibt es bei der Integralrechnung leider keinen. So gibt es einige Funktionen wie zum Beispiel \[ f(x) = e^{-x^2} \] die man nicht elementar integrieren kann.
Wir wollen nun einen Flächenbegriff einführen, der für die Integralrechnung sehr wichtig ist. Wir definieren eine Fläche, so wie man es sich vorstellt, mit der Ausnahme, dass eine Fläche im eigentlichen Sinne immer positiv ist. Eine negative Fläche kann man sich räumlich nicht vorstellen. In der Mathematik sprechen wir aber von der orientierten Fläche.
Dies wollen wir an folgender Skizze kurz verdeutlichen. Hier haben wir eine die Funktion $f(x)=2$, die oberhalb der $x$-Achse liegt, und die Funktion $f(x)=-2$, die unterhalb der $x$-Achse liegt.

Die rot markierte Fläche beträgt $2 \cdot 3 = 6$ FE. Die blau markierte Fläche hat betraglich gesehen den gleichen Flächeninhalt. Da sie aber unterhalb der $x$-Achse liegt, erhält die blaue Fläche ein negatives Vorzeichen. Die orientierte Fläche ist demnach $-6$ FE groß.
Wenn wir nun die beiden Flächen addieren, so erhalten wir $6 + (-6) =0$. Dies ist im ersten Moment etwas ungewohnt, da man denkt, dass die beiden Flächen zusammen 12 FE groß sind. Hier muss man immer aufpassen, was für eine Fläche man betrachtet. In der Integralrechnung betrachten wir nur orientierte Flächen. Dies bedeutet, dass das Integral auch nur orientierte Flächen angibt. Will man also die typische Fläche bestimmen, also beispielsweise bei Anwendungsaufgaben, so muss man die Nullstellen der Funktion herausfinden und dann die Fläche getrennt berechnen.
Hierzu kommen wir aber erst später.
Beginnen wir mit der Berechnung der Fläche unter einer Kurve. Nun kommt die Frage auf, wie wir das machen können? Um diese Frage zu beantworten fangen wir mit einem einfachen Beispiel an. Hierzu betrachten wir eine sehr einfache Funktion und zwar die konstante Funktion $f(x)=2$.
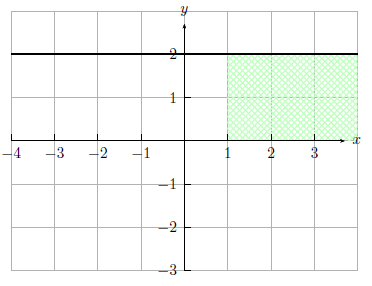
Wenn wir nun die Fläche zwischen Graphen und der $x$-Achse im Intervall $[1,4]$ bestimmen wollen, so können wir dies sehr schnell machen. \[ \text{Fläche } = \text{ Länge } \cdot \text{ Breite } \] heißt die Lösung in diesem Fall, da wir einfach nur die Fläche eines Rechtecks bestimmen wollen. Also erhalten wir die Fläche zu: \[ A = (4-1) \cdot 2 = 3 \cdot 2 =6 \] Unsere gesuchte Fläche ist also 6 Flächeneinheiten (FE) groß.
Aber wie gehen wir bei komplizierteren Funktionen vor? Wenn wir eine Gerade haben, die nicht konstant ist, so könnte man die Fläche unterhalb der Geraden noch mittels Dreiecken bestimmen. Wie sieht es aber bei einer Parabel aus? Betrachten wir also die Fläche im Intervall [1,4] unter dem Graphen von $f(x)=x^2$

Eine Idee wäre es, die Fläche in drei Teilintervalle zu unterteilen: $[1,2]$, $[2,3]$ und $[3,4]$. Nun können wir die einzelnen Flächen etwas annähern, indem wir nur das Rechteck unterhalb der Funktion in jedem Flächenabschnitt bestimmen. Also wie in der nächsten Skizze zu sehen ist.

Für die einzelnen Teilflächen brauchen wir die Breite, diese ist hier bei allen gleich 1, und die Höhe. An diese kommen wir mittels der $y$-Werte an der linken Grenze im jeden Teilintervall, also $f(1)$, $f(2)$ und $f(3)$, wie man leicht im Bild sehen kann. Demnach folgt für eine Näherung der gesuchten Fläche \[ \underline{A}_3 = A_1 + A_2 + A_3 = 1 \cdot f(1) + 1 \cdot f(2) + 1\cdot f(3) = 1^2+2^2+3^2 = 1 +4 +9 =14 \] Also haben wir als Annäherung eine Fläche von 14 FE. Der genauer Wert liegt bei 21 FE. Also haben wir noch einen recht großen Fehler. Im nächsten Abschnitt werden wir eine Möglichkeit sehen, womit wir die gesuchte Fläche besser eingrenzen können.
Anders als bei der Differentialrechnung, wo man einen Algorithmus zum Ableiten angeben konnte, gibt es bei der Integralrechnung leider keinen. So gibt es einige Funktionen wie zum Beispiel \[ f(x) = e^{-x^2} \] die man nicht elementar integrieren kann.
Wir wollen nun einen Flächenbegriff einführen, der für die Integralrechnung sehr wichtig ist. Wir definieren eine Fläche, so wie man es sich vorstellt, mit der Ausnahme, dass eine Fläche im eigentlichen Sinne immer positiv ist. Eine negative Fläche kann man sich räumlich nicht vorstellen. In der Mathematik sprechen wir aber von der orientierten Fläche.
Orientierte Fläche
Bei der orientierten Fläche unterscheidet man zwischen dem positiven und dem negativen Teil.
- Die Fläche zwischen einer Funktion $f$ und der $x$-Achse, die oberhalb der $x$-Achse liegt, ist positiv.
- Die Fläche zwischen einer Funktion $f$ und der $x$-Achse, die unterhalb der $x$-Achse liegt, ist negativ.

Die rot markierte Fläche beträgt $2 \cdot 3 = 6$ FE. Die blau markierte Fläche hat betraglich gesehen den gleichen Flächeninhalt. Da sie aber unterhalb der $x$-Achse liegt, erhält die blaue Fläche ein negatives Vorzeichen. Die orientierte Fläche ist demnach $-6$ FE groß.
Wenn wir nun die beiden Flächen addieren, so erhalten wir $6 + (-6) =0$. Dies ist im ersten Moment etwas ungewohnt, da man denkt, dass die beiden Flächen zusammen 12 FE groß sind. Hier muss man immer aufpassen, was für eine Fläche man betrachtet. In der Integralrechnung betrachten wir nur orientierte Flächen. Dies bedeutet, dass das Integral auch nur orientierte Flächen angibt. Will man also die typische Fläche bestimmen, also beispielsweise bei Anwendungsaufgaben, so muss man die Nullstellen der Funktion herausfinden und dann die Fläche getrennt berechnen.
Hierzu kommen wir aber erst später.
Beginnen wir mit der Berechnung der Fläche unter einer Kurve. Nun kommt die Frage auf, wie wir das machen können? Um diese Frage zu beantworten fangen wir mit einem einfachen Beispiel an. Hierzu betrachten wir eine sehr einfache Funktion und zwar die konstante Funktion $f(x)=2$.

Wenn wir nun die Fläche zwischen Graphen und der $x$-Achse im Intervall $[1,4]$ bestimmen wollen, so können wir dies sehr schnell machen. \[ \text{Fläche } = \text{ Länge } \cdot \text{ Breite } \] heißt die Lösung in diesem Fall, da wir einfach nur die Fläche eines Rechtecks bestimmen wollen. Also erhalten wir die Fläche zu: \[ A = (4-1) \cdot 2 = 3 \cdot 2 =6 \] Unsere gesuchte Fläche ist also 6 Flächeneinheiten (FE) groß.
Aber wie gehen wir bei komplizierteren Funktionen vor? Wenn wir eine Gerade haben, die nicht konstant ist, so könnte man die Fläche unterhalb der Geraden noch mittels Dreiecken bestimmen. Wie sieht es aber bei einer Parabel aus? Betrachten wir also die Fläche im Intervall [1,4] unter dem Graphen von $f(x)=x^2$

Eine Idee wäre es, die Fläche in drei Teilintervalle zu unterteilen: $[1,2]$, $[2,3]$ und $[3,4]$. Nun können wir die einzelnen Flächen etwas annähern, indem wir nur das Rechteck unterhalb der Funktion in jedem Flächenabschnitt bestimmen. Also wie in der nächsten Skizze zu sehen ist.

Für die einzelnen Teilflächen brauchen wir die Breite, diese ist hier bei allen gleich 1, und die Höhe. An diese kommen wir mittels der $y$-Werte an der linken Grenze im jeden Teilintervall, also $f(1)$, $f(2)$ und $f(3)$, wie man leicht im Bild sehen kann. Demnach folgt für eine Näherung der gesuchten Fläche \[ \underline{A}_3 = A_1 + A_2 + A_3 = 1 \cdot f(1) + 1 \cdot f(2) + 1\cdot f(3) = 1^2+2^2+3^2 = 1 +4 +9 =14 \] Also haben wir als Annäherung eine Fläche von 14 FE. Der genauer Wert liegt bei 21 FE. Also haben wir noch einen recht großen Fehler. Im nächsten Abschnitt werden wir eine Möglichkeit sehen, womit wir die gesuchte Fläche besser eingrenzen können.