Hauptsatz der
3HTAM Mathe-Hilfe online
Hauptsatz der Differential- und Integralrechnung
Nun kommen wir zu einem der wichtigsten Sätze der Differential- und Integralrechnung. Dieser Satz verbindet die beiden Themen und gibt uns eine sehr gute Beschreibung von einer
Fläche unter einer Kurve und vor allem, wie man sie dann auch ermitteln kann, ohne mit Unter- und Obersummen zu arbeiten.
Leider ist der Satz etwas theoretisch, aber ich bin der Meinung, dass es sehr wichtig ist, ihn einmal richtig verstanden zu haben. Deshalb gehen wir ganz detailliert und langsam vor, damit jeder Schritt verständlich ist. Also dann ran an die Herleitung des Hauptsatzes.
Leider ist der Satz etwas theoretisch, aber ich bin der Meinung, dass es sehr wichtig ist, ihn einmal richtig verstanden zu haben. Deshalb gehen wir ganz detailliert und langsam vor, damit jeder Schritt verständlich ist. Also dann ran an die Herleitung des Hauptsatzes.
Schritt 1
Wir betrachten die Fläche $S$, die die untere Grenze $x$ und die obere Grenze $x + \Delta x$ besitzt. Mit $\Delta x$ ist ein beliebiger Wert $> 0$ zu verstehen.

Die Fläche $S$ geben wir nun mit den Integralfunktionen, die wir kennen gelernt haben, an.
Zur Erinnerung: Die Integralfunktionen $J_0(x)$ gibt die Fläche mit der unteren Grenze $0$ und der oberen Grenze $x$ an.
Betrachten wir nun die Skizze, so können wir die markierte Fläche angeben mit:
Dies erkennt man an den folgenden Skizzen sehr gut:
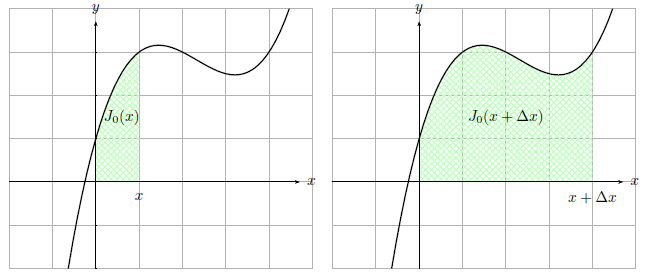

Die Fläche $S$ geben wir nun mit den Integralfunktionen, die wir kennen gelernt haben, an.
Zur Erinnerung: Die Integralfunktionen $J_0(x)$ gibt die Fläche mit der unteren Grenze $0$ und der oberen Grenze $x$ an.
Betrachten wir nun die Skizze, so können wir die markierte Fläche angeben mit:
1. Hilfssatz
\[S = J_0(x + \Delta x) - J_0(x)\]

Schritt 2
Als Nächstes betrachten wir die Untersumme $\underline{A}_1$ und die Obersumme $\overline{A}_1$ von $S$. Diese bestehen genau aus einem einzigen Balken (und nicht mehreren).
Hierfür wird einfach der Tief- beziehungsweise Hochpunkt der Funktion bestimmt. Somit kann man gut die beiden Summen zeichnen.

Hierbei ist $f(\underline{x})$ der kleinste Funktionswert im Intervall $[x , x+\Delta]$ und $f(\overline{x})$ der größte Funktionswert im selben Intervall. Nun gilt offensichtlich, dass die gesuchte Fläche zwischen den beiden Flächen $\underline{A}_1$ und $\overline{A}_1$ liegt. Mit anderen Worten gilt:
Bemerkung: Da die Fläche eines Rechteckes immer Länge mal Breite ist, haben wir in der Ungleichung die jeweiligen Ausdrücke.
$\Delta x$ ist in beiden Fällen die Länge und $f(\underline{x})$ beziehungsweise $f(\overline{x})$ sind die Breiten.
Hierfür wird einfach der Tief- beziehungsweise Hochpunkt der Funktion bestimmt. Somit kann man gut die beiden Summen zeichnen.

Hierbei ist $f(\underline{x})$ der kleinste Funktionswert im Intervall $[x , x+\Delta]$ und $f(\overline{x})$ der größte Funktionswert im selben Intervall. Nun gilt offensichtlich, dass die gesuchte Fläche zwischen den beiden Flächen $\underline{A}_1$ und $\overline{A}_1$ liegt. Mit anderen Worten gilt:
2. Hilfssatz
\[f(\underline{x}) \cdot \Delta x \leq S \leq f(\overline{x}) \cdot \Delta x\]
Schritt 3
Nun haben wir die Vorarbeit geleistet und zwei Formeln für die Fläche $S$ kennen gelernt. Setzen wir die erste Formel in die zweite Formel ein, so erhalten wir:
\[f(\underline{x}) \cdot \Delta x \leq J_0(x + \Delta x) - J_0(x) \leq f(\overline{x}) \cdot \Delta x \]
Nun teilen wir die Ungleichung durch $\Delta x$. Dies können wir ohne Probleme machen, da dieser Wert $>0$ ist. Somit haben wir nun folgende Ungleichungskette:
\[f(\underline{x}) \leq \frac{J_0(x + \Delta x) - J_0(x)}{ \Delta x} \leq f(\overline{x}) \]
Der mittlere Ausdruck ähnelt sehr dem Differentialquotienten
\[f'(x_0)=\lim\limits_{h\rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h}. \]
Identifizieren wir $h$ mit $\Delta x$ und die Funktion $f$ mit der Integralfunktion $J_0$, so ist er einzige Unterschied, dass wir bei der Ungleichung $\Delta x$ noch nicht gegen Null haben laufen lassen.
Was passiert nun wenn wir $\Delta x$ gegen Null laufen lassen? Der Differentialquotient geht gegen $J'_0(x)$.
Und wohin gehen der linke und rechte Ausdruck? Wird der Abstand zwischen den $x$-Werten immer kleiner, so wird auch der Unterschied der Funktionswerte immer kleiner. Da $\Delta x \to 0$ gilt, folgt $f(\underline{x}) = f(\overline{x})$ welches wiederum gleich $f(x)$ wird. Demnach folgt die Vorstufe des Hauptsatzes.
Was passiert nun wenn wir $\Delta x$ gegen Null laufen lassen? Der Differentialquotient geht gegen $J'_0(x)$.
Und wohin gehen der linke und rechte Ausdruck? Wird der Abstand zwischen den $x$-Werten immer kleiner, so wird auch der Unterschied der Funktionswerte immer kleiner. Da $\Delta x \to 0$ gilt, folgt $f(\underline{x}) = f(\overline{x})$ welches wiederum gleich $f(x)$ wird. Demnach folgt die Vorstufe des Hauptsatzes.
Vorstufe des Hauptsatzes
\[J'_0(x) = f(x)\]
Schritt 4 - Der Hauptsatz der Differential- und Integralrechnung
Nun kommen wir zum letzten Punkt. Betrachten wir die Vorstufe des Hauptsatzes und bilden auf beiden Seiten die Stammfunktion, so erhalten wir mit den Konstanten $c,d$ und $e \in \mathbb{R}$:
\begin{align}
J_0(x) + d &= F(x) + e &&|-d\\
J_0(x) &= F(x) + e -d &&|c:= e-d\\
J_0(x) &= F(x) +c &&
\end{align}
Nun betrachten wir das Integral von $a$ nach $b$ von der Funktion $f(x)$; hierbei sei $a = x$ und $b= x + \Delta x$. Demnach ist das Integral unsere Fläche $S$. Mit dem ersten Schritt unserer Herleitung folgt nun:
\[ S = \int_a^b f(x) ~\mathrm dx = J_0(b) - J_0(a) \]
Setzen wir nun unsere Beziehung $J_0=F(x)+c$ in diese Gleichung ein, so erhalten wir:
\[ \int_a^b f(x) ~\mathrm dx = F(b) + c - \left( F(a)+c \right) = F(b) - F(a) \]
Dies ist auch schon unser Hauptsatz.
Der Hauptsatz mit anderen Worten:
Der Hauptsatz der Differential- und Integralrechnung ist ein Hilfsmittel, um die Fläche unter einer Funktion zu bestimmen. Bisher musste man immer nur über den Umweg der Ober- und Untersummen gehen, was ein wenig kompliziert und nervig ist. Nun beschränkt sich die Arbeit auf das Finden einer Stammfunktion. Haben wir eine gefunden, so müssen wir nur noch obere und untere Grenze einsetzen und die Differenz betrachten.
Nun noch ein kleines Rechenbeispiel, um auch Fragen zu klären, wie man so etwas aufschreibt. Sei hierzu $f(x)=2x+1$. \begin{align} \int_1^4 2x +1~\mathrm dx = \bigl[\underbrace{x^2 +x}_{F(x)}\bigr]_1^4 = \underbrace{(4^2+4)}_{F(4)} - \underbrace{(1^2+1)}_{F(1)} = 20 - 2 = 28 \end{align}
Hauptsatz der Differential- und Integralrechnung
Die Funktion $f$ sei auf dem Intervall $I$ stetig. Ist $F$ eine beliebige Stammfunktion von $f$ in $I$, dann gilt für alle $a \in I$ und $b \in I$:
\[ \int_a^b f(x) ~\mathrm dx = F(b) - F(a)\]
Der Hauptsatz der Differential- und Integralrechnung ist ein Hilfsmittel, um die Fläche unter einer Funktion zu bestimmen. Bisher musste man immer nur über den Umweg der Ober- und Untersummen gehen, was ein wenig kompliziert und nervig ist. Nun beschränkt sich die Arbeit auf das Finden einer Stammfunktion. Haben wir eine gefunden, so müssen wir nur noch obere und untere Grenze einsetzen und die Differenz betrachten.
Nun noch ein kleines Rechenbeispiel, um auch Fragen zu klären, wie man so etwas aufschreibt. Sei hierzu $f(x)=2x+1$. \begin{align} \int_1^4 2x +1~\mathrm dx = \bigl[\underbrace{x^2 +x}_{F(x)}\bigr]_1^4 = \underbrace{(4^2+4)}_{F(4)} - \underbrace{(1^2+1)}_{F(1)} = 20 - 2 = 28 \end{align}