Differentialquotienten
3HTAM Mathe-Hilfe online
Ableiten mittels
Differentialquotienten
Was versteht man unter "Steigung in einem Punkt"? Dies ist den
Meisten nicht sofort klar. Sucht man nach einer Definition der
Steigung, so findet man in der Regel die Folgende:
Was machen wir in unserem Fall? Wir wollen ja nicht die Steigung von
der Verbindung zweier Punkte haben, sondern die Steigung in einem
Punkt. Um Begriff der Steigung zu verdeutlichen, schauen wir uns ein
Beispiel aus der Geschichte an.
Die Meisten kennen bestimmt das Beispiel von Newton und dem Apfel. Wir wollen nun die Geschwindigkeit des Apfels zu einem Zeitpunkt $t_0$ ermitteln. Da der Apfel beim Herabfallen nicht die gleiche Geschwindigkeit beibehält, sondern schneller wird, haben wir ein kleines Problem. Was ist eigentlich Geschwindigkeit? \[\text{Geschwindigkeit } = \frac{\text{Strecke}}{\text{Zeit}}\] Also messen wir die Strecke, die der Apfel in einer gewissen Zeit durchfliegt. Um ein paar konkrete Zahlen zu haben, nehmen wir an, wir wollen die Geschwindigkeit zum Zeitpunkt $t_0=1$ bestimmen. Nun messen wir nach einer Sekunde die zurückgelegte Strecke $s=3m$ und erhalten für unsere Durchschnittsgeschwindigkeit $v$ \[ v = \frac{3 m}{1 s} = 3 \frac{m}{s}. \] Wie euch bestimmt aufgefallen ist, habe ich nicht Geschwindigkeit, sondern Durchschnittsgeschwindigkeit gesagt, da der Apfel beim Fallen immer schneller wird. Um nun die Geschwindigkeit zum Zeitpunkt $t_0$ zu berechnen, müssen wir nun immer genauer messen. Also die Zeitabstände immer kürzer wählen. Ideal wäre es natürlich, dass der Zeitunterschied nahezu Null ist. Mathematisch ausgedrückt heißt dies: \[ \lim\limits_{t_1\rightarrow t_0} \] Diese Schreibweise ist auf dem ersten Blick ein wenig ungewöhnlich, wird aber manchmal verwendet. $\lim$ steht für den Limes und bedeutet in diesem Fall, dass ich das $t_1$, unser zweiter Zeitpunkt, gegen $t_0$, unseren ersten Zeitpunkt, laufen lasse. Wenn für diesen Fall, also immer kleinere Zeitabstände, der Quotient $\frac{\text{Strecke}}{\text{Zeit}}$ gegen einen Wert kleiner unendlich läuft, so nennen wir dies die Geschwindigkeit zum Zeitpunkt $t_0$.
Nun wollen wir dasselbe Spiel nochmal an einer Funktion betrachten. Dazu nehmen wir uns die Funktion $f(x)=x^2$ und berechnen die Steigung in $(1|1)$. Grafisch könnte man sagen, dass die Steigung in dem Punkt gleich der Steigung der Tangente an $(1|1)$ ist. Gut, nun können wir zeichnerisch die Steigung berechnen, aber wie machen wir dies rechnerisch?
Unsere Grundidee ist es, dass wir keine Tangente betrachten, sondern eine Sekante (im folgenden Bild grün); also eine Gerade die unsere Funktion in 2 Punkten schneidet. Neben unseren Punkt $(1|1)$ schneidet sie die Funktion in $(x|f(x))$. Nun können wir die Sekantensteigung $m$ berechnen: \[m= \frac{f(1)-f(x)}{1-x} \]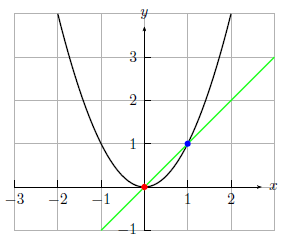
Wenn wir nun den Punkt $(x|f(x))$ entlang der Funktion $f(x)$ zum Punkt $(1|1)$ laufen lassen, so nähern wir uns immer mehr der Steigung der Tangente an. Man kann auch sagen, dass wir die Sekante um den festen Punkt $(1|1)$ so drehen, dass die Sekante zur Tangente wird. Dieses Laufen lassen bezeichnen wir, wie oben schon, mit dem Limes. Mit diesem anschaulichen Beispiel erhalten wir die folgende Definition zur Steigung in einem Punkt.
Hat der Differentialquotient einen Grenzwert, also einen Wert kleiner
als unendlich, so heißt die Funktion $f(x)$ an der Stelle
$x_0$ differenzierbar.
Der Differentialquotient gibt die
Tangentensteigung an der Stelle $x_0$ an. Lässt man im obigen
Ausdruck das Limes weg, so erhält man nur die Steigung der
Sekante. $ \frac{f(x)-f(x_0)}{x-x_0}$ wird dann Differenzenqoutient
genannt.
Hinweis: Oft sieht man auch folgenden äquivalenten Ausdruck für den Differentialquotienten und bei Existenz des Grenzwertes auch für die Steigung: \[ f'(x_0)=\lim\limits_{h\rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} \] Der zweite Ausdruck ergibt sich, indem man $x=x_0+h$ setzt.
Um zu unserer Funktion zurückzukommen erhalten wir die folgende Tangente (rot):
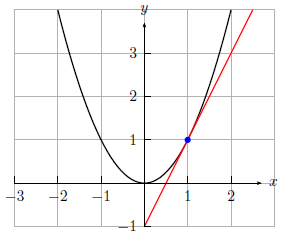
Wie wir im letzten Abschnitt gesehen haben, kann man mittels Differentialquotienten die Steigung einer Funktion in einem Punkt berechnen. Nun versuchen wir mittels dieser Definition die Steigung von $f(x)=x^2$ in $(1|1)$ rechnerisch zu ermitteln. Dazu schreiben wir erst einmal die Definition auf und erhalten \[ f'(1)= \lim\limits_{x \to 1} \frac{f(x) - f(1)}{x-1} = \lim\limits_{x \to 1} \frac{x^2 - 1}{x-1}. \] Nun kommen wir zur Stelle, wo die meisten ihre Probleme haben. Bis hierhin ist alles nur einsetzen gewesen. Das Problem ist nun, wenn wir $x$ gegen 1 laufen lassen, teilen wir durch Null. Dies bedeutet, dass wir irgendwie versuchen müssen den Bruch zu kürzen, sodass anschließend im Nenner keine Null mehr steht. In diesem Fall schaffen wir es mit der 3. binomischen Formel, denn $(x-1) \cdot (x+1) = x^2-1$. Setzen wir dies oben ein, so liefert dies \[ f'(1) = \lim\limits_{x \to 1} \frac{\color{red}{(x-1)} \cdot (x+1)}{\color{red}{x-1}} = \lim\limits_{x \to 1} x+1 = 2. \] Zum Schluss konnten wir einfach $x=1$ einsetzen, da wir nicht mehr durch Null geteilt haben. Somit ist die Steigung in $(1|1)$ gleich 2.
Steigung einer Geraden
Die Steigung $m$ einer Geraden mit den zwei Punkten $(x_1|y_1)$ und
$(x_2|y_2)$ ist definiert als
\[ m = \frac{y_2-y_1}{x_2-x_1}.\]
Die Meisten kennen bestimmt das Beispiel von Newton und dem Apfel. Wir wollen nun die Geschwindigkeit des Apfels zu einem Zeitpunkt $t_0$ ermitteln. Da der Apfel beim Herabfallen nicht die gleiche Geschwindigkeit beibehält, sondern schneller wird, haben wir ein kleines Problem. Was ist eigentlich Geschwindigkeit? \[\text{Geschwindigkeit } = \frac{\text{Strecke}}{\text{Zeit}}\] Also messen wir die Strecke, die der Apfel in einer gewissen Zeit durchfliegt. Um ein paar konkrete Zahlen zu haben, nehmen wir an, wir wollen die Geschwindigkeit zum Zeitpunkt $t_0=1$ bestimmen. Nun messen wir nach einer Sekunde die zurückgelegte Strecke $s=3m$ und erhalten für unsere Durchschnittsgeschwindigkeit $v$ \[ v = \frac{3 m}{1 s} = 3 \frac{m}{s}. \] Wie euch bestimmt aufgefallen ist, habe ich nicht Geschwindigkeit, sondern Durchschnittsgeschwindigkeit gesagt, da der Apfel beim Fallen immer schneller wird. Um nun die Geschwindigkeit zum Zeitpunkt $t_0$ zu berechnen, müssen wir nun immer genauer messen. Also die Zeitabstände immer kürzer wählen. Ideal wäre es natürlich, dass der Zeitunterschied nahezu Null ist. Mathematisch ausgedrückt heißt dies: \[ \lim\limits_{t_1\rightarrow t_0} \] Diese Schreibweise ist auf dem ersten Blick ein wenig ungewöhnlich, wird aber manchmal verwendet. $\lim$ steht für den Limes und bedeutet in diesem Fall, dass ich das $t_1$, unser zweiter Zeitpunkt, gegen $t_0$, unseren ersten Zeitpunkt, laufen lasse. Wenn für diesen Fall, also immer kleinere Zeitabstände, der Quotient $\frac{\text{Strecke}}{\text{Zeit}}$ gegen einen Wert kleiner unendlich läuft, so nennen wir dies die Geschwindigkeit zum Zeitpunkt $t_0$.
Nun wollen wir dasselbe Spiel nochmal an einer Funktion betrachten. Dazu nehmen wir uns die Funktion $f(x)=x^2$ und berechnen die Steigung in $(1|1)$. Grafisch könnte man sagen, dass die Steigung in dem Punkt gleich der Steigung der Tangente an $(1|1)$ ist. Gut, nun können wir zeichnerisch die Steigung berechnen, aber wie machen wir dies rechnerisch?
Unsere Grundidee ist es, dass wir keine Tangente betrachten, sondern eine Sekante (im folgenden Bild grün); also eine Gerade die unsere Funktion in 2 Punkten schneidet. Neben unseren Punkt $(1|1)$ schneidet sie die Funktion in $(x|f(x))$. Nun können wir die Sekantensteigung $m$ berechnen: \[m= \frac{f(1)-f(x)}{1-x} \]

Wenn wir nun den Punkt $(x|f(x))$ entlang der Funktion $f(x)$ zum Punkt $(1|1)$ laufen lassen, so nähern wir uns immer mehr der Steigung der Tangente an. Man kann auch sagen, dass wir die Sekante um den festen Punkt $(1|1)$ so drehen, dass die Sekante zur Tangente wird. Dieses Laufen lassen bezeichnen wir, wie oben schon, mit dem Limes. Mit diesem anschaulichen Beispiel erhalten wir die folgende Definition zur Steigung in einem Punkt.
Differentialquotient
Der Differentialquotient einer Funktion $f$ an der Stelle $x_0$
ist definiert als \[ f'(x_0)=\lim\limits_{x\rightarrow x_0}
\frac{f(x)-f(x_0)}{x-x_0}. \]
Hinweis: Oft sieht man auch folgenden äquivalenten Ausdruck für den Differentialquotienten und bei Existenz des Grenzwertes auch für die Steigung: \[ f'(x_0)=\lim\limits_{h\rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} \] Der zweite Ausdruck ergibt sich, indem man $x=x_0+h$ setzt.
Um zu unserer Funktion zurückzukommen erhalten wir die folgende Tangente (rot):

Wie wir im letzten Abschnitt gesehen haben, kann man mittels Differentialquotienten die Steigung einer Funktion in einem Punkt berechnen. Nun versuchen wir mittels dieser Definition die Steigung von $f(x)=x^2$ in $(1|1)$ rechnerisch zu ermitteln. Dazu schreiben wir erst einmal die Definition auf und erhalten \[ f'(1)= \lim\limits_{x \to 1} \frac{f(x) - f(1)}{x-1} = \lim\limits_{x \to 1} \frac{x^2 - 1}{x-1}. \] Nun kommen wir zur Stelle, wo die meisten ihre Probleme haben. Bis hierhin ist alles nur einsetzen gewesen. Das Problem ist nun, wenn wir $x$ gegen 1 laufen lassen, teilen wir durch Null. Dies bedeutet, dass wir irgendwie versuchen müssen den Bruch zu kürzen, sodass anschließend im Nenner keine Null mehr steht. In diesem Fall schaffen wir es mit der 3. binomischen Formel, denn $(x-1) \cdot (x+1) = x^2-1$. Setzen wir dies oben ein, so liefert dies \[ f'(1) = \lim\limits_{x \to 1} \frac{\color{red}{(x-1)} \cdot (x+1)}{\color{red}{x-1}} = \lim\limits_{x \to 1} x+1 = 2. \] Zum Schluss konnten wir einfach $x=1$ einsetzen, da wir nicht mehr durch Null geteilt haben. Somit ist die Steigung in $(1|1)$ gleich 2.